Stats Menu
When designing an experiment you should have an idea of how you will analyze the data after it is collected. This way you will not conduct the experiment and then find out you did not collect data in an appropriate way to analyze it.
Although not considered statistical tests, the following procedures will be helpful as you begin the analysis of patterns in a data set.
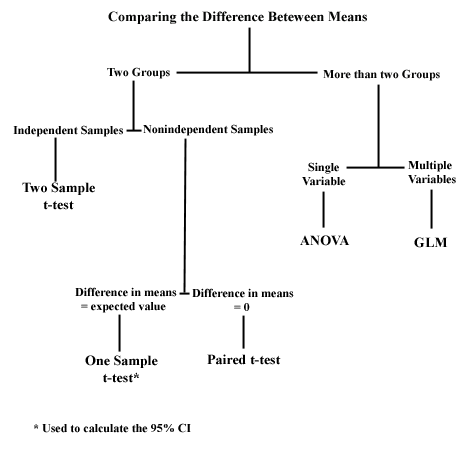
Often an experiment is designed to determine the difference caused by an experimental variable.
For most of the experiments you will be doing we will assume the data form a normal distribution (bell-shaped curve) and parametric statistics can be used. If the data are not normally distributed you will need to consult with your instructor and use one of the slightly less sensitive, non-parametric statistical tests.
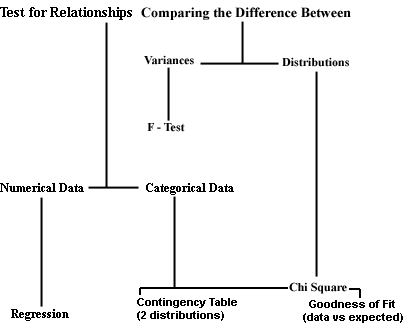
A summary of the major tests used in Biology 109 is given below. By clicking on a test name you will be linked to information on when to apply it, how to organize the data in Minitab, and how to interpret the test results. Use back to return to this chart.
 |
|
| ******Calculating descriptive statistics: use this to summarize data and get a sense of variability. |
Stat ->Basic Statistics -> Display Descriptive Statistics -> Variable (select all the columns you want to have the statistics calculated for).
Using a Code Column to Calculate Descriptive Statistics: use this to divide the data in a single column into several treatments based on the codes in the code column.
Stat -> Basic Statistics -> Display Descriptive Statistics -> Variable LDC (data column) -> By Variable (after selecting this option) -> LDC (code column)
The following information will be displayed in the session window:
N = the # of individuals in the sample (the total # of students in the sample).
MEAN = the average (e.g.. the average resting pulse rate if you specified C1).
MEDIAN = the middle value; 50% of values (e.g.. pulse rates) are above, 50% below the median. If N is an odd #, then the median is, in fact, the middle value; if N is an even #, then the median is half way between the two middle values.
TRMEAN = the 5% trimmed mean. First the data are sorted - lowest to highest. Then the lowest 5% and the highest 5% of the values are discarded; the remaining 90% are averaged to give the trimmed mean. Use of the trimmed mean allows one to discard the most extreme values that may fall well outside of the range of the majority of values in the sample.
STDEV = the standard deviation, the average deviation of the individual measurements from the mean - a measure of how spread out the data are. Recall that for a normal distribution 68% of the data values fall between one standard deviation above and one standard deviation below the mean.
SEMEAN = the standard error of the mean. It is the standard deviation divided by the square root of N. The standard error is a particularly useful measure of the variation in a sample, preferable to standard deviation in most cases.
MIN = the minimum or smallest value (e.g.. lowest resting pulse rate in the sample for C1).
MAX = the maximum or highest value (highest resting pulse rate in the sample for C1
Q1 and Q3 = the first or lower quartile and the third or upper quartile. The MEDIAN is the second quartile. The three quartiles divide the data into four, essentially equal parts. Thus Q1-Q3 (the interquartile range) defines the area in which the middle 50% of the values of the sample are located. In a perfect Normal Distribution the MEAN and MEDIAN are the same, thus the middle 50% of the values are evenly distributed to either side of the MEAN.
Graph Menu -> Interval Plot -> one Y-variable with groups -> Graph variable (Enter the column containing the data), Categorical variable (Enter the code)
The graph will contain error bars that represent the 95 % confidence interval.
If the 95% confidence intervals of the two means overlap considerably it is unlikely that they will be found to
be significantly different when they are compared using the appropriate statistical test.
Editing the graph for presentation in a paper. Also refer to page 10 in your lab manual.
• With cursor on graph LC to select graph. LC and drag from corner to resize.
• LCH then drag to reposition graph.
• LC to select and edit axis labels
• LC to select and delete information above graph.
• Use (T ) from editing tool pallet to add a text box under the graph for a caption. Back
| ******Determining the 95% confidence interval: use to calculate the 95% CI. Data must be in separate columns. |
Stat -> Basic Statistics -> 1 sample t -> options -> conf interval (enter 95%)
This command calculates the range for the 95% confidence interval. Means from repeated samples representing the group under study should fall within this range 95% of the time. To express the 95% confidence interval as a single number simply subtract the mean from the high value of the interval. In graphs and tables data can be summarized as the mean ± 95% confidence interval. Sometimes in tables you will see a mean and the range of the 95% confidence interval. Back
| ******F-test: use this test to determine if the variances in two samples are significantly different. |
Stat -> Anova -> Test for Equal Variances -> Response (enter the data column) -> Factor (enter the code column). Confidence interval assumes 95%.
The F statistic is calculated by dividing the larger variance by the smaller one. F= (s21) /(s22).
If the value of F exceeds the critical value for samples of the size under study (p<05) reject the null hypothesis of no difference. If p > .05 you must conclude that there is no significant difference in the variances or that the variances are homogeneous (equal). Back
Data column and a code column
Stats -> Basic Statistics -> 2 sample t -> Samples in one column -> Samples (enter data column) -> Subscripts (enter code column). (Check "Assume equal variance")
Data in separate columns
Stats -> Basic Statistics -> 2 sample t -> Samples different Col -> First (enter 1st data column)-> Second (enter 2nd data column ). (Check "Assume equal variance")
Minitab responds to these commands by displaying first the N, mean, standard deviation and the standard error for the two samples. Then below this information it displays the statement '95 PCT CI FOR MU C# - MU C#:' followed by 2 numbers enclosed in parentheses. This is the 95% confidence interval for the difference between the two means (MU 1 - MU 2). This means that, given the variance observed, 95 out of 100 repeated comparisons between the two samples would have mean differences in the interval described. If this confidence interval includes 0 (e.g. -1.5 to +1.3) then you cannot claim the two means are significantly different. The final line of the display is: TTEST MU C# = MU C# (VS NE): T= (the calculated t value) P= (the probability level) DF= (the number of degrees of freedom). P is the probability that the difference between the two means is 0. The probability must be <0.05 to reject the null hypothesis of no difference between the means. Scientists generally reject the null hypothesis at a probability (significance level) of 5% or less. Back
Stats -> Basic Statistics -> Paired t -> (enter columns containing paired data)
Generally enter the column you expect to have the higher value first.
Sometimes the samples we want to compare are not independent so a two sample t-test is not appropriate. The growth rates of trees taken in two successive years are are not independent since they were taken on the same individual. You can think of these measurements as being paired and a paired t-test is appropriate for comparing them if they are normally distributed. The Ho for this test is meanafter = meanbefore (eg. The growth rate is the same in both years. Restated: meanafter - meanbefore = 0). This test calculates the difference in the two means and and compares it to zero.
Minitab responds to a paired t-test by displaying first the N, mean, standard deviation and the standard error for the two samples as well as for the difference between them. It also gives the range for the 95% confidence interval for the mean difference, the T statistic calculated for the mean difference and the P value. P is the probability that the mean difference between the two means is 0. The probability must be <0.05 to reject the null hypothesis that the difference in the means is zero. Back
| ******1 Sample t-test use this to compare a sample mean to an expected value, which you can specify. Data must be entered in a single column. |
Stats -> Basic Statistics -> 1 sample t -> Variables (enter data columns)-> Check "Test of Mean" (enter value in box ).
Minitab will respond with Test of mu = (value you entered) vs mu not = (value you entered). Below this will be printed the N, mean, standard deviation, standard error, T statistic, and P value.
P is the probability that the mean for the data equals the value you were comparing it to. The probability must be <0.05 to reject the null hypothesis that there is no difference in the mean for the data and the stated value. Note: If you calculated the difference between two non-independent means and specified the value for the difference as zero. This test would be like a paired t-test. The advantage of this test is that it lets you set the value you want to compare the data to. Back
Data stacked into a single column with a corresponding code column
Stats -> Anova -> Oneway -> Response -> LDC (enter data column) -> Factor -> LDC (enter code column).
Data unstacked and in several columns
Stats -> Anova -> Oneway -> Unstacked (enter the columns containing the data)
Background on Analysis of Variance Often it is desirable to compare more than two groups. Analysis of variance allows you to determines wether one or more means are significantly different from any of the other means. First, consider some background on this test so that you can understand the results provided by MINITAB. Suppose you want to determine if cover affects pine height. You might begin by calculating the standard deviation for the height of all the trees. If you square this standard deviation you will get the variance for these data. This value of variance is for the whole data set, without separating the trees into the different cover levels (experimental groups). This is called total variance. Individuals within experimental groups are not all identical. They vary. This is called within-group variance (or error). Individuals in different experimental treatments may vary in a consistent pattern. When having different experimental groups adds to total variance, then we can measure between-group (or factor) variance. The total variance is the sum of the within and between group variance. Analysis of variance determines these different components of total variance and calculates the F ratio:
F = Factor variance (between group)/Error variance (within group).
The F ratio basically tells us whether our experimental grouping has much influence, as compared to variation we would see without having experimental differences. The common-sense approach is that with more variation caused by experimental factors the F ratio will be larger. Like t-values, the F ratio has critical values that must be exceeded before we can reject our statistical null hypothesis of "no experimental effect."
Minitab responds to the analysis of variance command with a table labeled "ANALYSIS OF VARIANCE" which has several columns. The left column names the possible SOURCEs of variance - FACTOR (between-group effects), ERROR (within-group effects), and TOTAL (the overall variance). The next column to the right shows the degrees of freedom; for example df for the group effect is the number of experimental groups minus one. The next column is the "sum of squares" or SS - the variance contributed by each source. The "MS" or "mean square" column is especially important because this is the variance scaled by the degrees of freedom; intuitively, it says how much variance is added for each item in the source line.
F ratio = MS for FACTOR (activity) / MS for ERROR
A significance level for the F ratio is provided. If P < 0.05, then the chances are less than one in twenty of getting the calculated F without having a real experimental effect.
Finally, below the ANOVA table, the means for each experimental group are given. A graph provides a quick visual view of the 95% confidence intervals for the mean pulse of each group, allowing us to see where significant differences are likely to be found. If a confidence interval overlaps the mean of a second group, this suggests that chance alone produces the observed differences in mean pulse values. Back
Make sure you read the information below before doing this test.
Stat -> ANOVA -> General Linear Model -> Response (enter column with dependent variable) -> Model (enter the two columns with the factor codes separated by a vertical bar)
There are several different models that can be used to calculate a two way analysis of variance. The model given above is known as a General Linear Model (GLM). You can refer to this test as a GLM in your assignments. The model takes the form shown below.
GLM C#(dependent variable) = C#(factor 1) C#(factor 2) C#(factor 1)*C#(factor 2)
To use this model you must have a complete design that includes all possible combinations of the two factors under study. A good way to check this is to create a table (Table 1.)
Table 1. A table can be used to determine all possible combinations of
factors used to create a complete experimental design. In this 2 x 2 design there are two variables (factors) that
combine to make four possible treatments.
| Factor 1 yes | Factor 1 no | |
| Factor 2 yes | Treatment 1 = Factor 2 yes, Factor 1 yes | Treatment 3 = Factor 2 yes, Factor 1 no |
| Factor 2 no | Treatment 2 = Factor 2 no, Factor 1 yes | Treatment 4 = Factor 2 no, Factor 1 no |
A complete design allows you to answer three questions about the dependent variable
1. Does factor 1 significantly affect the variable?
2. Does factor 2 significantly affect the variable?
3. Is there a significant interaction between the two factors?
In Minitab the model can be abbreviated as: GLM C# = C# (factor 1) | C# (factor 2). Including the vertical bar is critical if you want the Minitab to calculate the p value for the interaction term.
When a GLM is done Minitab responds with a table very similar to that is provided for a one-way analysis of variance except that it has a line that gives the F and P values for each factor and one for the interaction term. This tells you whether your factors have an effect on the dependent variable of interest, but it does not tell you what the effect is or how large it is. There is no graph to help you visualize the relationship between the variables. There are two ways to visualize the relationship. Minitab can create an interaction plot or you can use descriptive statistics to sort the data and make a graph using Excel.
To create an interaction plot of a GLM using Minitab
Stat -> ANOVA -> Interaction Plot -> Response (enter column with dependent variable) -> Factors ( first enter the column for the factor you want to be used to generate the lines in the graph then enter the column for the factor that you want to be used for the x axis) -> Data Means
To sort the data from a GLM in preparation for making an Excel Interaction Graph
Stats -> Basic Statistics -> Variable (enter the column with the data) -> By Variable (enter the combined code column) -> LC Statistics -> LC SEMean -> OK -> OK
To create interaction plots in Excel, it is necessary to calculate the means ± SE for all possible combinations of the factors used in the experiment (Table 1). Minitab requires that the data used in calculating a GLM are stacked in one column and different code columns are used for each factor. It is not possible to calculate descriptive statistics on the data by two factors at the same time. For this reason a 'combined' code column should be created. This column should have a code for each combination of factors. This 'combined' code column can be used as the By variable when calculating descriptive statistics. If you want to have the computer calculate the means, SEMean and store it in a column so you can paste the data into Excel use the following:
Alternatively you could unstack the data using the combined code column and calculate the 95% CI. - If you decide to use the 95% confidence interval. I suggest you unstack just one column at a time to make it easier to keep track of what you are doing. The number of columns required to receive the data will depend on the number of different codes in the code column. TAs/instructors will be happy to help you sort this out.
To Report a Two Way Analysis of Variance
In the simplest case you will have two variables with two different levels of each. When reporting the results of a GLM give the F value and P value for each factor and the interaction. By examining the size of the F value the reader has a sense of what proportion of the variation is caused by each factor.
If both factors are significant and there is a significant interaction, a complete reporting of the results requires that you point out the nature of the interaction. Since this is often difficult to interpret make your figure and then consult your instructor.
To calculate Chisquare using untabulated data
Stat -> Tables -> Cross Tabulation -> Classification Variables (enter the two columns of data to be tabulated giving the variable for the rows then the variable for the columns) Check "Chisquare Analysis", "Above and expected counts" (this will result in a table that contains both the observed and expected counts.
To calculate Chisquare using tabulated data
Stat -> Tables -> Chi Square -> Columns containing the table (enter the two or more columns that contain the table). The designation for the row variables are not entered in a column.
Minitab will print a table that contains the observed values (the ones you counted) on top and the expected values below (the ones you would get if the two variables were independent). The Chi Square value, degrees of freedom (df) and the p value will be printed under the table. If p 0.05 then the two variables are not independent.
An example is given below. It examines the relationship between winter conditions and the probability a tree will be browsed by deer. In this analysis we are dealing with "categorical data" - the number of trees that fit into different categories. We will use data from 1992-1993 since this is the period when deer were most apt to browse leaders. Whether a tree is browsed or not defines two categories. Whether a tree was browsed in 1992 or 1993 defines two additional categories. Essentially, we would like to know whether the frequency of trees that were browsed is independent of the year.
The statistical test that allows us to test for independence of categories is a
CHI SQUARE TEST. A simplified example is shown below. In each cell, the number on top is the observed
frequency of trees for the combination of categories indicated. The number in parentheses in each cell is the number
of observations that are expected according to the "null hypothesis" -which is that the categories
are independent of one another.
|
Year |
Not Browsed | Browsed | Total (spacing) |
|
1992 |
10 (8.75) |
15(16.25) |
25 |
|
1993 |
25 (26.25) |
50 (48.75) |
75 |
| TOTAL for browsing |
35 |
65 |
100 (grand total) |
The "expected" number, based on independence is calculated as follows:
(total of row)*(total of column)]/(total observations)
The formula for calculating Chi Square is simply based on adding up deviations from expected (squared to make them positive numbers) scaled by the magnitude of the expected value.
Chi Square = [ (observed-expected) 2 /expected]
The Chi Square value is compared to a table of critical values to determine whether the observed pattern could be expected by chance. If the calculated value is greater than the critical value, then there is a significant deviation (e.g., P<0.05) from independence. In other words, we would conclude that a biological relation exists between the categories. If you get a significant deviation, then the next step is to examine the nature of the pattern. Did more browsing occur in 1992 than 1993? You need to go back to the data to answer this question.
When reporting results from a Chi Square Test include the test name, df, and the X2 value. If your results indicated that the two variables are not independent you could present the proportion in each category or calculate the percent above or below the expected value. Back
Stat -> Tables -> Chi Square Goodness of fit -> Observed counts (enter column) -> Category names (enter column with names) -> Specific proportions (enter column with proportions)
When reporting results from a Chi Square Goodness of Fit Test include the test name, df, and the X2 value. If your results indicated that the data deviate significantly from the expected proportion calculate the percent above or below the expected value or simply report the magnitude of the deviation.
Stats -> Regression (optional Fitted Line Plot) -> Response (data for Y) -> Predictor (data for X) -> Ok
Minitab responds to this command by printing the equation for the line defined by the data. The equation takes the form:
Y = a + bX.
a = the point where the line crosses the y-axis b = the slope of the line (Y/X)
Under the equation are the results of two t-tests. These test the null hypothesis that the slope and intercept
are equal to zero. If p.05 the slope or intercept are significantly different from zero.
The Analysis of Variance test reported with the regression determines if the slope is significantly different from zero. If p .05 you must reject the null hypothesis. This would mean there is support for the alternate hypothesis that the data are linearly related as described by the equation. If you are unable to reject the null hypothesis then you must conclude that there in no linear relationship between the two variables. In addition the regression determines the degree to which the data fit the line by calculating the coefficient of determination (r2) The coefficient of determination indicates the amount of variance explained by the line. This can range from 0-100% The closer to 100% the better the fit.
When reporting the results of a regression give the R2 value and the equation for the line and the p value for the ANOVA.