Animal Behavior ‑ Second
Midterm Examination ‑ Fall 2008
READ THESE INSTRUCTIONS: The test has three sections. You will answer 3
questions (33 points each); you will answer one question from each
section. DO NOT EXCEED ONE PAGE,
DOUBLE-SPACED ON EACH QUESTION. If you exceed 1 page, points will be deducted.
Section I.
Everyone must answer this question:
A. What does it mean for an animal
to behave optimally? What are the steps involved in constructing a model of
optimal behavior? What must be measured in order to construct any such model?
An animal
behaves optimally when its behavior maximizes the ratio of benefits over costs,
or, maximizes benefits and minimizes costs. For example, an animal behaving
optimally might forage for the most food it could (a benefit) while minimizing
time and energy (a cost). The idea of optimality also enters into other facets
of behavior, such as mate selection and courtship. Animals are not necessarily
making these calculations, such as the benefit of increased nourishment versus
cost of energy expended, but animals who can behave in a way that best balances
costs and benefits will have survival and reproductive advantages over those
who do not. In this way, natural selection chooses optimal behaviors within
a population.
To construct
an optimality model, a researcher must first define a range of possible behaviors
for the animal in question (After all, a behavior cannot be optimal if the
animal cannot perform it.). Second, the researcher must choose what to measure
as an indication of costs and benefits. This “currency” must be somehow related
to fitness, either directly, such as measuring number of young, or indirectly,
such as measuring energy content of food (which would lead to increased survivorship
and increased fitness). Third, the researcher must measure costs and benefits
of each of the possible behaviors, using as much quantification as possible
via the chosen currency. Finally, the researcher can create an optimality
model, by defining the relationships between the measured costs and benefits,
and can make a prediction based on the point in the model where ratio of benefits
over costs is maximized. As stated above, in an optimality model, the benefits
and costs of all possible behaviors in a given circumstance must be measured
in terms of a chosen currency that relates to fitness.
Section II. Answer of ONE the following (either B or C):
B. What is the coefficient of relatedness? How does it relate to the concept of Inclusive Fitness? Be sure to include explanations of Direct and Indirect Fitness. How many cousins would it be worth throwing overboard for one half-sibling? Explain your calculation.
p= possible pathways L= connections
necessary
Fig
1. Coefficient of relatedness
p r=Ć(0.5)L n=1
Sewall Wright, a population geneticist from the mid-1900’s is credited for both his studies of genetic drift and his calculations of the genetic-relatedness of any two individuals. This is called the coefficient of relatedness (r) and it is used to calculate the probability that two individuals from the same species share an allele by common descent.
r (fig. 1) essentially helps to explain seemingly altruistic behavior in which one individual acts in the interest of others at a cost to one’s self or one’s own fitness. As put forth by W.D. Hamilton, individuals act in an altruistic fashion if they are closely related; the higher the r value between an individual and others, the more it “pays” to act altruistically. This is a mathematical model termed Hamilton’s rule in which the following must be true: rB > C (r= relatedness, B= benefit to the recipient of the altruism, C= cost of the donor). On a genetic level, if one sacrifices oneself for a sibling with higher reproductive success (RS) with half of one’s genes also present in the sibling, then twenty-five percent of the one’s genes will survive in the offspring of the sibling.
This is related to inclusive fitness; the overall genetic contribution to subsequent generations of one’s own breeding success plus the effect of its behavior on the breeding success of others which share its genes by common descent. This is calculated by summing the direct fitness (RS through one’s offspring) and indirect fitness (RS through kin’s offspring).
J.B.S. Haldane, a pioneering population geneticist and a witty Briton, was quoted as saying, “would I lay down my life to save my brother? No, but I would to save two brothers or eight cousins”, while this may seem to be merely a statement exhibiting keen British humor, genetically speaking, two brothers (Ćr= 2*0.5= 1) is the same as eight cousins (Ćr=8*0.125=1). Haldane would be equally pleased with making the claim that he would be willing to save two cousins (Ćr=0.125*2=0.25) at the cost of one half-sibling (Ćr=0.25) since in sum both two cousins and one half-sibling are equal.
C. What is the polygyny threshold model? What does it
explain? How does it work? Use a figure to illustrate your answer.
When territory quality (and hence resource availability and/or quality) differs (see Figure 1), the first female (A) should choose the best territory possible (the high-quality territory 1) in order to maximize her reproductive success, which means entering into a monogamous relationship. Should a second female (B) come along, she should also choose a territory based upon maximizing reproductive success, and therefore, she should choose to find a new high-quality territory (territory 2) and also enter into a monogamous relationship. The cost of entering into a polygynous relationship and having to share resources outweighs any benefits, since female B’s reproductive success is greater if she chooses a different male in a different territory. A third female to come along (C) has two choices: a high-quality territory already inhabited by another female or an uninhabited, low-quality territory. Based upon the desire to maximize reproductive success, the third female should choose the high-quality territory, as her reproductive success will be higher here. The benefit of increased reproductive success outweighs the cost of sharing the territory and hence the resources with another female. In this sense, we say that the polygyny threshold (the point at which polygyny is more beneficial) has been crossed. In general, increased variability in territory quality leads to an increased likelihood of polygyny, while less variability leads to an increased likelihood of monogamy.
Section III. Answer of ONE the following (D or E):
D. Explain Figures 2 and 3a from Cratsley and Lewis (2003)
and use these figures to explain sexual selection in terms of Zahavi’s Handicap
principle. 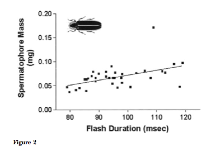
Zahavi’s handicap hypothesis suggests that traits selected in mating systems involving sexual selection should be honest indicators of an individual’s quality, and producing the trait should have a disadvantage (handicap) to the bearer. The traits should be costly to produce and the signal should not be easily faked, so that individuals cannot produce false signals.
Figure 2 of Cratsley and Lewis (2003) shows that in wild fireflies, male spermatophore mass is positively correlated with flash duration. Spermatophore mass is indicative of male quality because it is energetically costly to divert nutrients into larger spermatophores. Males that can do so are either physiologically higher quality and able to sacrifice more nutrients, or they are better foragers and acquire more nutrients. This trait cannot be faked, because an abundance of nutrients is essential to produce large spermatophores. Larger spermatophores are beneficial to females because they provide nutrients that are distributed to the eggs. Eggs with more nutrients should produce better quality offspring. Since females do not eat, the only way of increasing nutrition for the offspring is through choosing males with larger spermatophore mass. Thus, flash duration is an honest signal of male quality through a trait that will benefit offspring. Longer flashes likely take more energy to produce because emitting more light requires more energy. Thus, a male in poor energetic condition could not waste energy to “fake” a longer flash, just as a male could not fake large spermatophores.
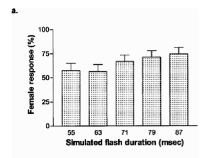
Figure 3 shows that females are more likely to respond to longer artificial flashes in the laboratory. Combined together, these two figures indicate that in the firefly mating system, females choose males with longer flashes because their gametes will contribute to higher quality eggs and therefore better survival of offspring. Thus, this finding is a confirmation of Zahavi’s hypothesis because a relatively non-falsifiable trait in males is chosen by females to improve the quality of her offspring.
E. Does Figure 2 from Bates and Chappell (2002) show that cultural transmission can be maladaptive? Use the figure to explain the concept of cultural transmission and how Bates and Chappell tested the hypothesis that such learning can be maladaptive (what does maladaptive mean?) and how to interpret their results.
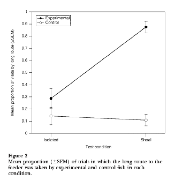
Bates and Chappell felt that Laland and Williams overlooked a critical test. They felt that the most appropriate experiment to determine if maladaptive behaviors could be culturally transmitted would be to see if individual “trained” guppies would take the long route to food if they had the choice of a shorter route. They hypothesized that there was some “predator defense benefit” for the guppies to remain in a group and that this benefit outweighed the costs of taking the long route (the maladaptive behavior of taking the long route was not as costly to fitnessas predation risk). They predicted that “trained” guppies should only take the long-route when in a group and not as individuals (there is a large benefit to being in a group). Figure 2 confirms their prediction.
They found that guppies only took the long route when in a “trained” group (87.5% of the time vs. 10-29% of the time for the three other groups). When an individual “trained” guppy was given a choice of route, it picked the shorter route the majority of the time. Figure 2 does show that a maladaptive behavior can be culturally transmitted (i.e. going the long route when they could go the short route is maladaptive). However, since trained isolated individuals took the short route, this shows that maladaptive behaviors can only be maintained if the benefits of another behavior being performed outweigh the maladaptive behavior’s costs (i.e. antipredation benefits of being in a group are more important to fitness than the maladaptive costs of taking the longer route).
E. Cultural transmission is the spread of information among individuals in a group. The advantages of cooperative behavior are that it allows animals to change their behavior quickly in rapidly-changing environments, and advantageous behaviors are spread quickly throughout the group. However, maladaptive behaviors can also be spread through the group quickly. According to Bates and Chappell (2002), maladaptive behaviors are those that "reduce the fitness of the receiver compared with the relative fitness of expressing an alternative behavioral pattern" (Introduction, 22).
Figure 2 shows that cultural transmission can be maladaptive for individuals, but does not support that it is maladaptive for groups. Control individuals took the long route less often than experimental individuals when they were alone. However, when shoaled, experimental individuals took the long route many more times than the control individuals because the experimental founders had taught the novel individuals to take the long route.
If the only cost were distance traveled to get food, and the only benefit were food obtained, then Figure 2 would support that cultural transmission was maladaptive. However, Bates and Chappell (2002) point out that the guppies may have incurred more benefits, such as lowered predation risk, by traveling as a group, even though they took a longer route to the food. If predation risk were high, the relative fitness of a guppy traveling in a group would be higher than the fitness of that same guppy traveling alone, so the behavior would be adaptive rather than maladaptive. On the other hand, if the guppies lived in a predator-free habitat, which would be rare, traveling in a group would confer no fitness benefit. The control individuals that took the shorter route would obtain more food and would therefore have higher relative fitness than the experimental individuals that took the longer route more often. Therefore, Figure 2 shows that cultural transmission could be adaptive or maladaptive, depending on the environmental risks.