Genetic Algorithms

The computer program first creates these digital chromosomes through stochastic (random) means, and then tests their "fitness". This can be done through one of two methods:

• Fitness-proportionate selection. This is a kind of genetic selection in which the computer would use a model or procedure to test the fitness of the chromosome and assign some kind of numeric value for its fitness in comparison to other chromosomes.
• Tournament selection. This form of selection involves "pitting" the chromosomes against each other in some kind of modeled environment. Those which survive the competition are deemed to be the fittest.

• Genetic recombination. This is analogous to sexual reproduction; new offspring are created from the fittest chromosomes of the previous generation.
• Mutation. This is analogous to the simulation of genetic mutation, in which the offspring are identical to their parents but have random, stochastic changes in their structure (and thus their traits are somewhat modified).

One interesting aspect of this computer-simulated darwinistic environment is that certain limiting factors such as an organism's life span or age of reproduction need not hinder the process of natural selection. For example, a parent's offspring could actually be inferior to the parent(s) because the process of reproduction may have made the offspring in such a way (e.g., if a mutation deleted a good trait or genetic crossing combined many bad aspects of each parents' genotypes). But because all of the chromosomes are ageless, the parent still stands just as good a chance of surviving over its offspring's generation.

This process of testing for fitness and creating new generations is repeated until the fittest chromosomes are deemed as optimized enough for the task which the genetic algorithm was created for. But what kinds of tasks could this kind of algorithmic be used for?

Uses of Genetic Algorithms
Genetic algorithms begin with a stochastic process and arrive at an optimized solution. Because of this, it will probably take much longer to arrive at a problem's solution through the use of a genetic algorithm than if a solution is found through analytical means and hardwired into the code of the computer program itself. For this reason, genetic algorithms are best suited for those tasks which cannot be solved through analytical means, or problems where efficient ways of solving them have not been found (Heitkoetter, Joerg and Beasley, Daveid, 1995). There exist a wide variety of such situations.

One excellent example is in the case of timetabling. In the University of Edinburgh, the scheduling for exams is calculated through the use of a genetic algorithm. Because each student has a different schedule and different priorities, it would be very difficult to design a conventional search and constraint algorithm for a computer program. Instead, a genetic algorithm is used in which each chromosome is originally a randomly-created exam timetable. The fitness function in the computer program simply tests each student's schedule into the timetable and rates the fitness of the timetable through several functions: how many conflicts there are, how many times a student has to take 2 consecutive exams, how many times a student has more than 3 exams in one day, and so on. This fitness function is used to test all the timetable chromosomes, and new generations are created, and eventually the optimized exam schedule is reached (Abramson & Abela 1991).

Genetic algorithms can be used in scientific design. For example if physicists had to design a turbine blade, they could make different chromosomes which had different genomes for properties of the blade such as the shape of the fan blade, its thickness, and its twist. The fitness function could then be a model which simulates the fan blade in different environments, and the algorithm could take the fittest blades and digitally interbreed them to arrive at the most optimum design (Taubes, 1997).

Quartet1 by Bruce L Jacob, arranged and composed using his variations 1 (occam) algorithm.

One very interesting use of this evolutionary algorithm has been developed in the field of music. Bruce L Jacob, a graduate student at the University of Michigan, recently developed a program which uses a special combination of genetic algorithms to compose music. The entire program consists of three modules. It begins with the COMPOSER module, which composes motives to phrases of music, each motive based on certain characteristics randomly defined by the COMPOSER's digital chromosomes (these digital chromosomes are actually created by Jacob himself, so that the resulting piece is suited to his musical tastes). The EAR module then analyzes each motive which the COMPOSER creates by testing their "fitness": it compares the motive to a particular EAR chromosome which defines a system of tonality and pitch. If the motive passes through the fitness test with no violations (i.e., it does not violate the system of tonality for that particular EAR chromosome) then it is added to the phrase. This process is repeated over and over again, with each phrase being evaluated using different EAR chromosomes, and each of the motives in the phrase being based upon different COMPOSER chromosomes. When this is done, the ARRANGER stochastically arranges these phrases and sends them to Jacob, who determines their "fitness" himself. The arrangements which are deemed to be fit are then genetically crossed and/or mutated, and eventually an entire work is created. It is interesting to note that Jacob uses his algorithm only to create the score for the music, not to generate the music itself; he has human instrumentalists play the actual music because he dislikes the canny and mechanical sound of synthesized instrumentation.

Excerpt from a movement of Hegemon Fibre by Bruce L. Jacob. Also arranged and composed using variations 1 (occam).

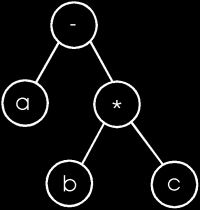Genetic Programming
One step beyond genetic algorithms is the field of genetic programming, in which the chromosomes are actual computer programs rather than data structures. In this case, the chromosomes have a variable length (as opposed to data structures which usually have a fixed length), and the genomes are represented as simple data structures which symbolize sub-trees of computer code and are arranged in a heirarchial order called a parse tree. This kind of concept is much easier to explain through diagrams. In the figure to the right, the algorithm a + (b * c) is expressed as a parse tree. Here the (b * c) is like a genome and the a + [B] is another genome. These algorithms are executed and whichever ones are deemed to be the most fit are cross-bred and sometimes mutated by switching around the genomes, or the sub-trees of the parse tree. This results in different and sometimes more efficient genomes. The operators in the parse tree make up what is called the function set, and can be any kind of function which is applicable for the task--i.e., they don't have to be addition/subtraction/etc, they can be actual binary functions which do some operation to both of its arguments. The arguments for the operators make up the terminal set. This kind of method is much closer to something that actually changes the behavior of a computer rather than simply a data structure inside the computer; in genetic algorithms, the variety of genomes are finite because their size is fixed and the interpretation of these genomes is based on the fitness function, which limits the evolutionary phenomenon of creativity. However, in genetic programming, the possibility for the variety of genomes is infinite because the size of the genome is of variable length and is executable code in itself. Thus it possibly brings us closer to a true kind of artificial intelligence.

The Field Programmable Gate Array (FPGA)
Recently, a very interesting development has arisen in the world of computing which has already heralded much progress for genetic algorithms and the field of artificial intelligence. Computers have always been divided into two halves, between the world of the software and hardware. This is because the hardware in a computer functions through transistors and the computer software sends different signals through them to simulate its own logic gates (e.g., in the form of IF..THEN statements). This simulation of logic gates in software is extremely slow in comparison to the hardwired logic gates of hardware, which is why users often have to upgrade their hardware to have their software run faster. Recently, however, a new kind of chip, called the Field Programmable Gate Array (FPGA), has been developed. This chip is essentially configurable hardware; it contains an array of values, each value representing a string of bits that can be set. These values are interpreted by the chip as potential logic gates. Thus the entire chip can be programmed by software to program itself into different configurations of logic gates to perform different tasks (Taubes 1997). This is the equivalent of a circuit re-wiring itself into different configurations!

In this way, the FPGA presents a way for computer engineers to design computers which re-wire their hardware; imagine not ever having to buy a new computer again! But what does this have to do with genetic algorithms and artificial intelligence?

If genetic algorithms use the array of configurable gates in an FPGA as their digital chromosome, then they can be used to "genetically evolve" the chip for a particular task. This has already been accomplished; at Stanford, Koza and Forrest Bennett evolved an FPGA to sort seven numbers by size. After fifty generations were created, a sorting algorithm was found which was incredibly faster than one patented 35 years ago.

Currently, the code for the genetic algorithm to reprogram the FPGA and test the fitness of it for a particular task must reside off-chip, in software. But if the algorithm were capable of being placed on-chip, then hardware and software would become conflated, and evolution would not be constrained to a static task: the genetic algorithm itself could be subject to change through evolution; ultimately, according to visionaries like Hugo de Garis, this could result in brain-like self-learning (Taubes 1997).

A Teramac custom computing board, located at BYU. It contains 27 PLASMA FPGA chips. Photograph courtesy Brigham Young University.

But the FPGA is not limited to the boolean world of digital technology when it wires itself; this is because the medium of silicon (which the FPGA is based on) is not limited between computing with the standard range of ones and zeros--it is also capable of producing an entire spectrum of values between the two values; in this way, the FPGA is not limited to the rules of digital design, but rather to the limits of natural physics. Adrian Thompson at the University of Sussex in the UK exploited this capability: he made a genetic algorithm which tested various configurations of the chip so that it would generate a 1 volt signal if it detected a 1-kilohertz audio tone and a 5 volt signal if it detected a 10-kilohertz audio tone. After a certain amount of evolution, the program worked brilliantly, but what is downright scary is this: the FPGA only used 32 of its 100 available logic gates to achieve its task, and when scientists attempted to back-engineer the algorithm of the circuit, they found that some of the working gates were not even connected to the rest through normal wiring. Yet these gates were still crucial to the functionality of the circuit. This means, according to Thompson, that either electromagnetic coupling or the radio waves between components made them affect each other in ways which the scientists could not discern (Taubes 1997). What this means for the world of artificial intelligence is that computers themselves can do things internally which even the human beings who designed them do not understand. Humans do not completely understand consciousness, and probably never will; but now who is to say that humans cannot design a self-evolving mesh of silicon which evolves into a self-conscious organism?

Of course, this is a rather bold statement and there are many skeptics who believe otherwise. But still, the concept that technology can evolve into something that its creators do not understand still gives artificial intelligence a bright star of hope; this topic, as to whether computers can be classified as life, will be explored in the next section entitled Artificial Life.

Copyright © 1997 Atool Varma and Nathan Erhardt.