The
Pink population reduced in population from approximately 30,000 Pinks
in the 7100s to fewer than 7,000 in the mid 7600s. After Reds
created underground reservations for the Pinks, the population
gradually stabilized to the 20,000 ranges by the year 7800.
However, the population ceased to stabilize and instead increased from
20,000 to over 50,000 by the time of Human discovery in the
7900s. The population has continued to increase at an exponential
rate from this time to present day. Now the Pink population is
larger than the Red population, and is barely able to be contained by
Underground reservation communities.
The problem is that researchers estimate that planetary resources cannot sustain any more than 170,000 Pinks and Reds. The Red population has petered out years ago at around 70,000 Reds with little growth. But the exponential growth of the Pink population is not ceasing. If this pattern of growth is maintained, life will be virtually unsustainable in less than 200 years.
Here are the projections:
If the population of Pinks in the year 7800 was only 20,000, and was 50,000 by 7912, then it only took 112 years for the population to increase by 40%.
If we use the standard equation for a population increase given the time it takes for a population to increase by a certain percent,
Nt= No * (1.4) ^ t/d
Where Nt is the population after t years, d is the number of years it takes for a population to increase by 40%, and No is the population in the year 7912.
Then,
Nt = 50,000 * (1.4) ^ t/ 88
If life will be unsustainable by the time that the Pink population reaches 100,000, then we can calculate how long that will take at this rate of exponential increase:
100,000 = 50,000 * (1.4)^t/88, solve for t, time,
t= ((log(100,000) – log(50,000))*88)/ log(1.4)
t= 181 years
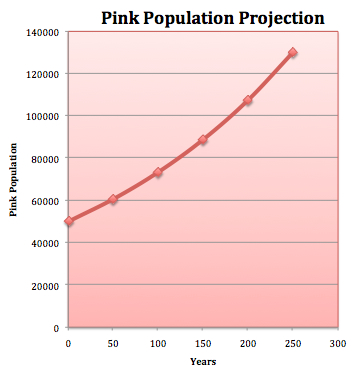
The problem is that researchers estimate that planetary resources cannot sustain any more than 170,000 Pinks and Reds. The Red population has petered out years ago at around 70,000 Reds with little growth. But the exponential growth of the Pink population is not ceasing. If this pattern of growth is maintained, life will be virtually unsustainable in less than 200 years.
Here are the projections:
If the population of Pinks in the year 7800 was only 20,000, and was 50,000 by 7912, then it only took 112 years for the population to increase by 40%.
If we use the standard equation for a population increase given the time it takes for a population to increase by a certain percent,
Nt= No * (1.4) ^ t/d
Where Nt is the population after t years, d is the number of years it takes for a population to increase by 40%, and No is the population in the year 7912.
Then,
Nt = 50,000 * (1.4) ^ t/ 88
If life will be unsustainable by the time that the Pink population reaches 100,000, then we can calculate how long that will take at this rate of exponential increase:
100,000 = 50,000 * (1.4)^t/88, solve for t, time,
t= ((log(100,000) – log(50,000))*88)/ log(1.4)
t= 181 years

How did this end up happening? See the theory.
About Heart
About The HCA
The People of Heart
The Pink Population Problem
The Theory
Proposed Solutions
What You Can Do
About Heart
About The HCA
The People of Heart
The Pink Population Problem
The Theory
Proposed Solutions
What You Can Do